고정 헤더 영역
상세 컨텐츠
본문
수능이 도대체 언제였는제 이제 올리느냐고 하실 수도 있겠습니다. 사실 풀기는 많이 풀었는데, 1문제 풀고 업로드 하기가 점점 귀찮아지더군요. 그래서 일단 충분히 많이 풀고 나서 업로드는 나중에 하자고 마음 먹은 터라 업로드가 좀 늦어졌습니다. 사진 하나만 업로드 하면 별로 어렵지 않은데 블로그 운영이라는 것이 글의 양이 충분해야 하는 압박이 있으므로 어쩔 수 없이 하루 한 문제 정도 업로드하는 것이 가장 현실적입니다.

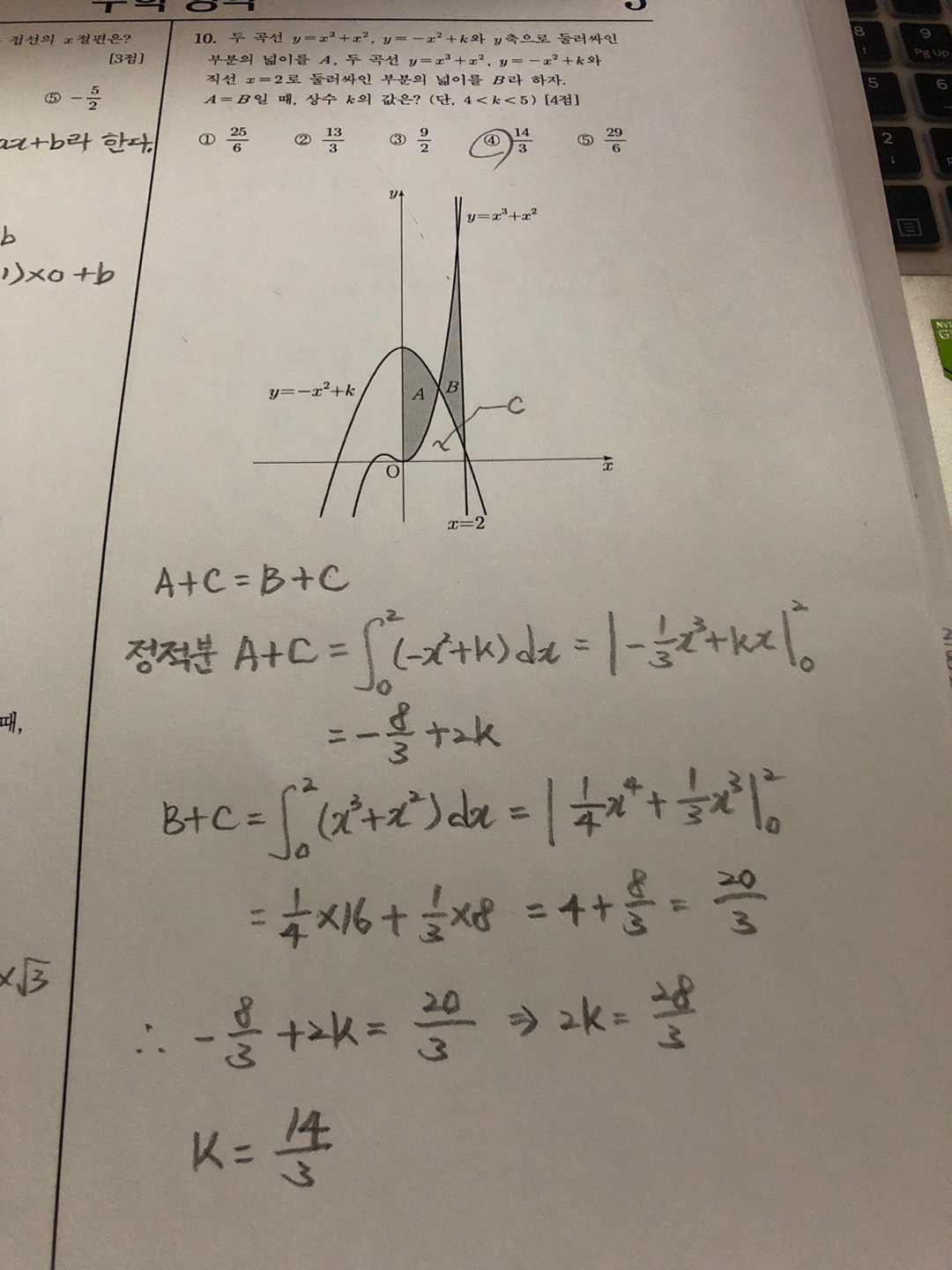
50살을 바라보는 엔지니어 아저씨가 취미로 푸는 수능 수학입니다. 2023년 수능 수학 10번 문제입니다. 이번 문제도 역시 풀다가 좌절했습니다. 정적분은 기억이 나고 다 알겠는데 문제가 풀리지 않아 며칠 고생했던 것 같습니다. 결국 가운데 비어있는 부분을 C라 하고 더해서 푸니까 풀리더군요. 곡선 함수를 빼서 정적분 했던 기억이 나는데 어떻게 풀었었는지 도무지 기억이 나지 않아 고생을 좀 했습니다.

어쨌든 이번에도 구글링의 도움을 받아 중간 부분을 C로 하고 푸는 방법이 있다는 것을 알게 되어 풀어보니 곧바로 풀리더군요. 다행히 면적 A 또는 B를 구하는 문제였으면 제가 푸는 과정이 맞았을 텐데, 상수 k만 구하면 되는 문제여서 그럴 필요가 애초부터 없었던 것인데 무리를 했던 것 같습니다.
정적분은 원리만 알면 정말 쉬운 부분입니다. 그리고 쉬운 만큼 실수하기 딱 좋은 개념이기도 합니다. 미분과 적분할 때 지수가 상수로 오는 것에서 가끔 실수를 하게 됩니다. 방법이 없고 그저 연습 또 연습하는 수밖에 없습니다. 그리고 다 푼 다음 반드시 2~3번 검산을 해봐야 합니다. 보통 너무 쉬워서 검산할 때도 넘어가는 경우도 있지만 그래도 검산을 하는 버릇을 들여야 합니다.
이번 기회에 적분과 정적분에 대한 정의부터 다시 살펴보겠습니다.
적분(積分, 영어: integral)은 정의된 함수의 그래프와 그 구간으로 둘러싸인 도형의 넓이를 구하는 것이다. 리만 적분에서 다루는 고전적인 정의에 따르면, 실수의 척도를 사용하는 측도 공간에 나타낼 수 있는 연속인 함수 f(x)에 대하여 그 함수의 정의역의 부분 집합을 이루는 구간 [a, b] 에 대응하는 치역으로 이루어진 곡선의 리만 합의 극한을 구하는 것이다. 이를 정적분(定積分, 영어: definite integral)이라 한다. 구간 [a, b]에 대하여 f(x) > 0이면 적분은 곡선의 면적과 동일하다. 그러나, 오른쪽 그림과 같이 구간 가운데 일부가 음수인 치역을 갖는다면 적분 값은 서로 상쇄되어 곡선이 이루는 면적과는 다를 수 있다.
그리고 미분과 적분에 기여하신 분들의 이름을 기억해주시길 바랍니다.
데카르트가 제시한 좌표 평면과 해석기하학의 출현은 미적분학이 발전하는 중요한 밑거름이 되었다. 아이작 뉴턴과 고트프리트 빌헬름 라이프니츠는 각자 독자적으로 미적분학을 수립하였으며 적분은 결국 미분의 역산으로 역도함수를 구하는 것과 같다는 점을 발견하였다. 이를 미적분학의 기본정리라고 한다. 19세기에 이르러 베른하르트 리만은 적분에 대해 수학적으로 엄밀한 정의를 내렸다. 1823년 오귀스탱 루이 코시는 모든 연속함수는 적분 가능함을 증명하였고, 리만은 이를 확장하여 연속 함수 f(x)의 적분은 해당 구간에서 리만 합의 극한과 같다는 점을 증명하였다. 이렇게 정의된 적분을 흔히 리만 적분이라 한다.
여러분이 잠깐 풀고 지나가는 미분과 적분에 정말 수많은 사람들의 연구 성과가 담겨 있답니다. 데카르트는 1500년대 사람이고 아이작 뉴턴은 1600년대 사람입니다. 이미 그때 미분과 적분의 개념이 태동하기 시작했고, 그때의 수학자들은 미분과 적분의 개념을 완벽하게 이해하고 있었습니다. 우리나라는 임진왜란으로 나라가 쑥대밭이 되던 때 지구 반대편에서는 미분과 적분을 풀고 있었다는 것이 참 신기합니다.
나이 많은 아저씨도 이렇게 노력하는데 젊거나 어린 분들 힘내세요. 시험 보신 수험생 여러분들은 정말 고생 많으셨습니다. 여러분들은 이미 대단하세요!
'잡학다식 & 자료 창고' 카테고리의 다른 글
| [엔지니어가 취미로 푸는 수학] 2023년 수능 수학 홀수형 공통 11번 문제 풀이 (1) | 2023.01.30 |
|---|---|
| 2023년 및 중기 경제전망 (0) | 2023.01.12 |
| 코로나 이후 디지털 전환과 경제·사회 미래전망 (0) | 2022.12.30 |
| 코로나19의 사회ㆍ경제적 영향 분석 및 「긴급재난소득」의 효과 평가 연구 (1) | 2022.12.29 |
| 영유아 문제행동지도를 위한 어린이집 보육교사 지침서 (0) | 2022.12.28 |





댓글 영역