고정 헤더 영역
상세 컨텐츠
본문

2023년 수능 수학 홀수형 공통 11번 문제 풀이입니다. 오랜만에 글을 업로드하는 것 같습니다. 수능이 끝나고 다음날 프린트해서 약 2개월 정도만에 전체를 다 풀었고 순서대로 업로드하겠습니다. 학력고사 세대인 저에게는 처음 접해보는 낯선 문제들도 있어서 공부하면서 푸느라 시간이 오래 걸렸습니다. 심지어 도저히 공부해도 모르겠길래 답을 보면서 공부한 문제도 있었습니다. 엔지니어 아저씨가 이 정도니 고등학생 여러분들은 이미 대단하십니다.
11번 문제는 원과 삼각형의 성질만 알면 됩니다. 원 위의 임의의 점에서 선분을 두 개 긋고 사이각을 이등분하면 이등분된 현과 호는 각각 길이가 같습니다. 원 위의 어떤 점에서도 성립하는 중요한 개념입니다. 그리고 결정적으로 그 유명한 사인 법칙과 코사인 법칙을 아는지를 묻는 문제입니다.
이 개념은 2천년 전에 쓰여진 유클리드 기하학이라고 불리는 유클리드의 ‘원론’의 공리에 의해 유도될 수 있을 정도로 유명한 개념입니다. 삼각형에서 코사인 법칙 또는 코사인 공식이라고도 하는 코사인 법칙은 기본적으로 삼각형의 길이를 각도 중 하나의 코사인과 관련시킵니다. 삼각형의 두 변의 길이와 그 사이의 각도를 알고 있으면 세 번째 변의 길이를 결정할 수 있습니다. 공식은 다음과 같습니다:
c^2 = a^2 + b^2 – 2ab cosγ
여기서 a, b, c는 삼각형의 변이고 γ는 a와 b 사이의 각도입니다. 아래 그림을 참고하세요.
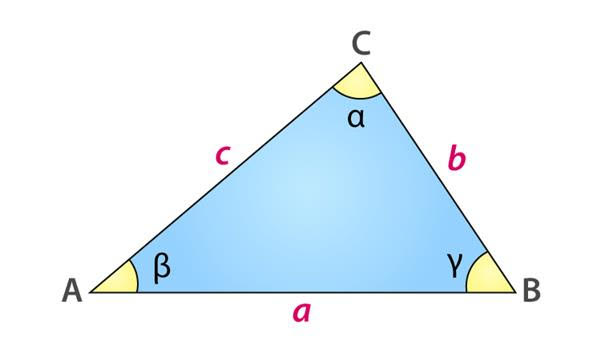
코사인 법칙 공식에 따라 삼각형의 변의 길이 △ABC를 구하려면 다음과 같이 쓸 수 있습니다.
- a^2 = b^2 + c^2 – 2bc cos α
- b^2 = a^2 + c^2 – 2ac cos β
- c^2 = b^2 + a^2 – 2ba cos γ
유도 과정을 굳이 복사하지는 않겠습니다. 수학의 정석, 참고서, 인터넷에 자세히 나와 있으니 찾아보시면 됩니다.
그리고 사인 법칙을 알아야 합니다. 사인 법칙은 삼각형의 변의 비율을 정의하고 각각의 사인 각도는 서로 동일하다는 개념입니다. 사인 법칙의 다른 이름은 사인 법칙, 사인 규칙 및 사인 공식입니다. 사인 법칙은 미지의 각도 또는 빗각 삼각형의 변을 찾는 데 사용됩니다. 비스듬한 삼각형은 직각 삼각형이 아닌 모든 삼각형으로 정의됩니다. 사인 법칙은 한 번에 적어도 두 개의 각도와 해당 측면 측정에 적용해야 합니다.
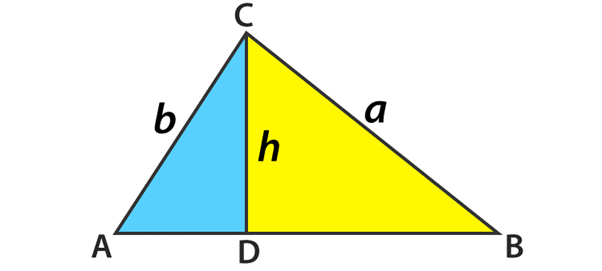
공식은 a / Sin A= b/ Sin B= c / Sin C, 또는 a: b: c = Sin A: Sin B: Sin C 입니다. 즉, 각각의 각도들의 사인 값의 비율과 마주보는 변의 길이의 비율이 같다는 의미입니다. 하지만 여기서는 굳이 사인 법칙까지 사용하지 않고 SinA = 1 / CosA로 풀어도 되니 편하신 대로 하시면 됩니다. 저는 그냥 편한 대로 풀었습니다. 다만 관련된 공식들은 모두 알고 계셔야 응용이 가능하므로 필요한 개념들은 소개하고 넘어가겠습니다.
'잡학다식 & 자료 창고' 카테고리의 다른 글
| [엔지니어가 취미로 푸는 수학] 2023년 수능 수학 홀수형 공통 13번 문제 풀이 (0) | 2023.02.01 |
|---|---|
| [엔지니어가 취미로 푸는 수학] 2023년 수능 수학 홀수형 공통 12번 문제 풀이 (0) | 2023.01.31 |
| 2023년 및 중기 경제전망 (0) | 2023.01.12 |
| [엔지니어가 취미로 푸는 수학] 2023년 수능 수학 홀수형 10번 문제 풀이 (0) | 2023.01.09 |
| 코로나 이후 디지털 전환과 경제·사회 미래전망 (0) | 2022.12.30 |





댓글 영역