고정 헤더 영역
상세 컨텐츠
본문

2023년 수능 수학 홀수형 공통 21번 문제 풀이입니다. 이번 문제는 로그 함수와 지수 함수에 대한 문제입니다. 정말 이제는 계산하는 기계가 되어서는 수학 문제를 풀 수가 없는 세상인 모양입니다. 이 문제는 반드시 저처럼 기하학적으로 그려봐야 이해가 되는 문제입니다. 문제는 짧은데 참 많이 생각하게 만드는 문제입니다. 솔직히 문제를 풀면서 복잡하게 꼬아 놓긴 했지만 문제 참 잘 만들었다는 생각이 들었습니다. 의미 없이 꼬아 놓기만 한 문제들이란 생각이 드는 문제들이 있는 반면에 이런 문제는 인정할 수밖에 없었습니다. 누가 낸 문제인지 출제자가 정말 똑똑한 것 같습니다. 이 문제는 꼬았지만 적당히 꼬아서 감당할 수 있는 정도의 수준입니다. 로그 함수와 지수 함수의 기본 개념을 알고 있는지, 그리고 기하학에 대한 기초가 있는지 묻고 있습니다. 21번 문제는 로그, 지수, 기하학에 약한 학생들은 일단 점수를 안 주겠다는 확실한 의도가 엿보입니다.
문제를 풀기 시작하자마자 문제에서 주어진 조건을 바로 이해할 수 있어야 합니다. 함수 f(x)는 0보다 작은 구간에서 지수함수, 0보다 크거나 같은 구간에서는 로그함수입니다. 그런데 공통적으로 두 함수 모두 n 만큼 아래로 움직였습니다. 게다가 두 함수 모두 절대값으로 f(x)는 음의 수는 가질 수 없습니다. 즉, 음수 부분이 x축을 기준으로 대칭으로 양의 값으로 바뀐다는 의미입니다. 그래서 그래프의 모양이 제가 그린 것처럼 변하게 되는 것입니다. 다시 정리해보겠습니다.



왼쪽부터 순서대로 설명하겠습니다. 맨 왼쪽 그림에서 지수함수와 로그함수는 원래 저렇게 생겼습니다. 서로 역함수 관계입니다. 하지만 문제에서 주어진 함수의 그래프가 정확하게 저렇게 생겼다는 의미는 아닙니다. 문제의 조건을 이해하는 데에만 참고하시기 바랍니다. 두 번째 그림에서 n 만큼 아래로 내린 후 조건에 맞게 지수함수의 양의 부분은 잘라냅니다. 로그함수는 x 값이 모두 양의 값이므로 잘라낼 필요가 없습니다. 만약 실제로 음의 부분이 있다면 지수함수와 마찬가지로 잘라내면 됩니다. 세번째 그림에서 절대값으로 인해 y의 음의 값을 양의 값으로 대칭 이동합니다. 이렇게 만들어진 그래프 모양을 빨간색으로 표현하면 위와 같습니다.
이제 그래프의 모양은 이해했고, 문제에서 f(x)=t의 실근의 개수가 g(t)라고 할 때 g(t)의 최댓값이 4가 되도록 하는 자연수 n을 찾으라고 했습니다. 말을 어렵게 해놨지만 x축과 평행하게 수평선을 하나 그어서 위의 그래프와 교점이 최대 4개가 되도록 하면 됩니다. 위의 그래프에서는 4개가 가능합니다. 제가 손글씨로 풀어놓은 그래프처럼 교점이 4개인 구간이 있으므로 가능합니다. 그런데 여기에서 문제는 최솟값이 아닌 최댓값이라는 점입니다. 그럼 반대로 최대 4개가 아닐 수도 있다는 것이라는 점을 이해해야 합니다.

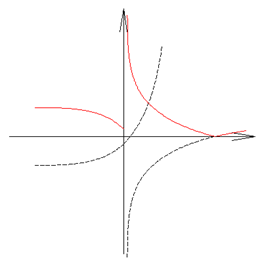
위 그림을 보시면, n 값이 과도하게 커져서 너무 밑으로 많이 내리고 나서 문제에서 주어진 조건을 적용해 보면 x축과 평행한 f(x)=t와의 교점의 최댓값은 4가 아닐 수 있습니다. 위 그림과 같이 2또는 3일 수 있습니다. 따라서 어느 한계 밑으로 그래프를 내리지 못하도록 n 값을 조절하라는 의미입니다. 그렇다는 것은 어느 점을 기준으로 대칭이 되는지, 즉, y=0인 점을 알기 위해 f(x)가 0이 되는 x 값을 찾아야 합니다. 바로 위 그림에서 지수함수는 x축과 교점이 없습니다. 즉, 지수함수는 x 축과의 교점이 항상 0보다 작아야만 v자 모양으로 그래프가 그려진다는 의미이고, 로그함수는 x축과의 교점이 항상 0보다 커야만 v자 모양으로 그래프가 그려진다는 뜻입니다. 두 그래프가 동시에 v자 모양으로 생겨야만 교점이 4개까지 나오기 때문입니다.
따라서 이제 두 함수의 x축과의 교점을 찾아서 그 교점이 지수함수는 0보다 작고, 로그함수는 0보다 크다는 조건식을 세워 n값을 구하기만 하면 됩니다. 이제부터는 쉽습니다. 곧바로 n의 범위가 2 < n < 9라는 것을 알 수 있습니다. 그리고 항상 말씀 드리지만, 자나깨나 실수 조심, 끝난 문제도 다시 보자! 문제에서 마지막에 뭘 구하라고 했죠? 자연수 n이 가질 수 있는 값들을 모두 더하라고 했습니다. 즉, 3~8까지 더하기만 하면 됩니다. 실수하도록 깨알같이 함정을 만들어 놨습니다. 정답은 모두 더해서 33입니다.
'잡학다식 & 자료 창고' 카테고리의 다른 글
| [엔지니어가 취미로 푸는 수학] 2023년 수능 수학 홀수형 공통 22번 문제 풀이 (0) | 2023.02.08 |
|---|---|
| 지속가능경영을 위한 기업 가이드 ESG A to Z (0) | 2023.02.08 |
| [엔지니어가 취미로 푸는 수학] 2023년 수능 수학 홀수형 공통 20번 문제 풀이 (0) | 2023.02.06 |
| [엔지니어가 취미로 푸는 수학] 2023년 수능 수학 홀수형 공통 19번 문제 풀이 (0) | 2023.02.05 |
| [엔지니어가 취미로 푸는 수학] 2023년 수능 수학 홀수형 공통 16번, 17번, 18번 문제 풀이 (0) | 2023.02.04 |





댓글 영역