고정 헤더 영역
상세 컨텐츠
본문

2023년 수능 수학 홀수형 미적분 25번 문제 풀이입니다. 이 문제는 극한 문제여서 미적분 문제로 분류된 것 같습니다. 사실 간단한 등비수열 문제입니다. 등비수열의 기본은 an = a1 X r^(n-1)입니다. 이것만 알아도 풀 수 있는 문제입니다. 극한 문제는 문제를 단순화시키는 능력이 중요합니다. 이 문제는 분자와 분모 모두 무한대로 발산하는 등비수열입니다.
an = a1 X r^(n-1)인 것을 알고 있으니 an=a1/r X r^n으로 생각할 수 있습니다. 이렇게 바꾸는 이유는 r을 가정하여 식을 단순화시키기 위해서입니다. 분모에서는 3^n과 4^n 두가지 지수함수가 있는데 경험적으로 밑수가 큰 수를 선택하는 것이 좋습니다. 지수 n이 무한대로 발산할 때는 공약수가 없다면 차라리 큰 수를 선택하는 편이 낫습니다. 따라서 r=4라고 하고 분자와 분모 모두를 4^n으로 나누면 식은 급격하게 단순화됩니다. 분모에서 (3/4)^n을 0으로 만들기 위해 4^n으로 나눠준 것을 알 수 있습니다. 다시 한 번 말씀 드리지만, 등비수열은 an = a1 X r^(n-1)입니다. 그리고 극한은 식을 어떻게 단순화시키느냐의 싸움입니다.
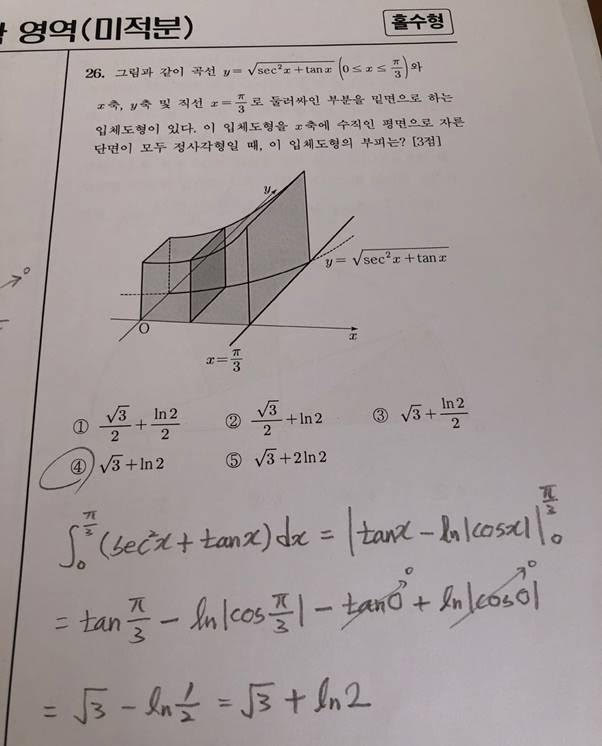
2023년 수능 수학 홀수형 미적분 26번 문제 풀이입니다. 문제가 복잡해 보이고 화려한 것에 비해 다소 허무한 문제였습니다. 오픈북으로 풀던 저도 책 집어 던지고 그냥 풀어낸 문제이기도 합니다. 며칠을 풀어봐도, 인터넷과 수학책을 뒤져봐도 도저히 모르겠다고 하면 정답 풀이과정을 검색해서 공부한 뒤 풀기도 하는데, 이런 문제는 아직은 끄떡 없습니다. 문제가 요즘은 3차원으로도 나오는 모양입니다. 그렇다고 쫄 필요는 없습니다. 적분의 기본 개념을 아는지 묻는 문제일 뿐 아무것도 아닌 문제입니다. 단지 도형이 3차원일 뿐이니 복잡하게 생각할 필요 없습니다.
문제를 말로 풀어 보면, 2차원 좌표 상의 함수가 있고 함수의 y값을 한 변으로 하는 정사각형을 3차원으로 그려서 3차원 도형으로 만들면 부피는 얼마냐고 묻는 문제입니다. 부피가 됐든 면적이 됐든 단순히 정적분으로만 풀면 됩니다. 그래프의 면적을 구할 때 아주 작은 단위로 잘라서 더하는 것을 적분으로 정의하므로 여기에 한 번 더 곱해서 정사각형의 면적을 구해주기만 하면 됩니다. 그래서 함수가 루트로 씌워진 것입니다. 그러니 삼각함수인 시컨드와 탄젠트를 적분할 줄 아느냐고 묻는 것과 같습니다. 역시 저는 기억이 안 나서 인터넷으로 기본 적분 공식을 찾아보고 풀었습니다. 삼각함수의 미분과 적분 공식은 기본적으로 외워두는 것이 좋습니다. 문제를 많이 풀다 보면 저절로 외워지기도 합니다. 여기까지만 풀어 내면 그 다음부터는 단순 적분 문제로 바뀝니다. 굳이 설명하지 않아도 아실 거라고 믿습니다.
'잡학다식 & 자료 창고' 카테고리의 다른 글
| [엔지니어가 취미로 푸는 수학] 2023년 수능 수학 홀수형 미적분 28번 문제 풀이 (0) | 2023.02.23 |
|---|---|
| [엔지니어가 취미로 푸는 수학] 2023년 수능 수학 홀수형 미적분 27번 문제 풀이 (0) | 2023.02.20 |
| [엔지니어가 취미로 푸는 수학] 2023년 수능 수학 홀수형 미적분 23번, 24번 문제 풀이 (0) | 2023.02.17 |
| [엔지니어가 취미로 푸는 수학] 2023년 수능 수학 홀수형 확률과 통계 30번 문제 풀이 (0) | 2023.02.15 |
| [엔지니어가 취미로 푸는 수학] 2023년 수능 수학 홀수형 확률과 통계 29번 문제 풀이 (0) | 2023.02.14 |





댓글 영역