고정 헤더 영역
상세 컨텐츠
본문
엔지니어가 취미로 푸는 수학
2023년 수능 수학 홀수형 기하학 29번 문제 풀이
2023년 수능 수학 홀수형 기하학 29번 문제 풀이입니다. 풀다 보니 저에게는 기하학이 쉬운 편인 것 같습니다. 좋아하기로는 미적분을 좋아하는데 풀기에는 기하학이 쉬운 것 같은 느낌입니다. 개인적인 느낌일 뿐이니 참고만 하시기 바랍니다. 사실 공대생 입장에서는 기하학도 중요하지만 미적분이 가장 중요해서 일종의 의무감 같은 것이 있어 공부해야 할 것 같은 느낌이 강하게 들기도 합니다. 그리고 제가 미적분을 워낙 좋아했었기 때문에 약간 애착도 있습니다. 하지만 2023년 수능 수학 시험에서는 기하학이 상대적으로 쉽다는 느낌이 강하게 듭니다.
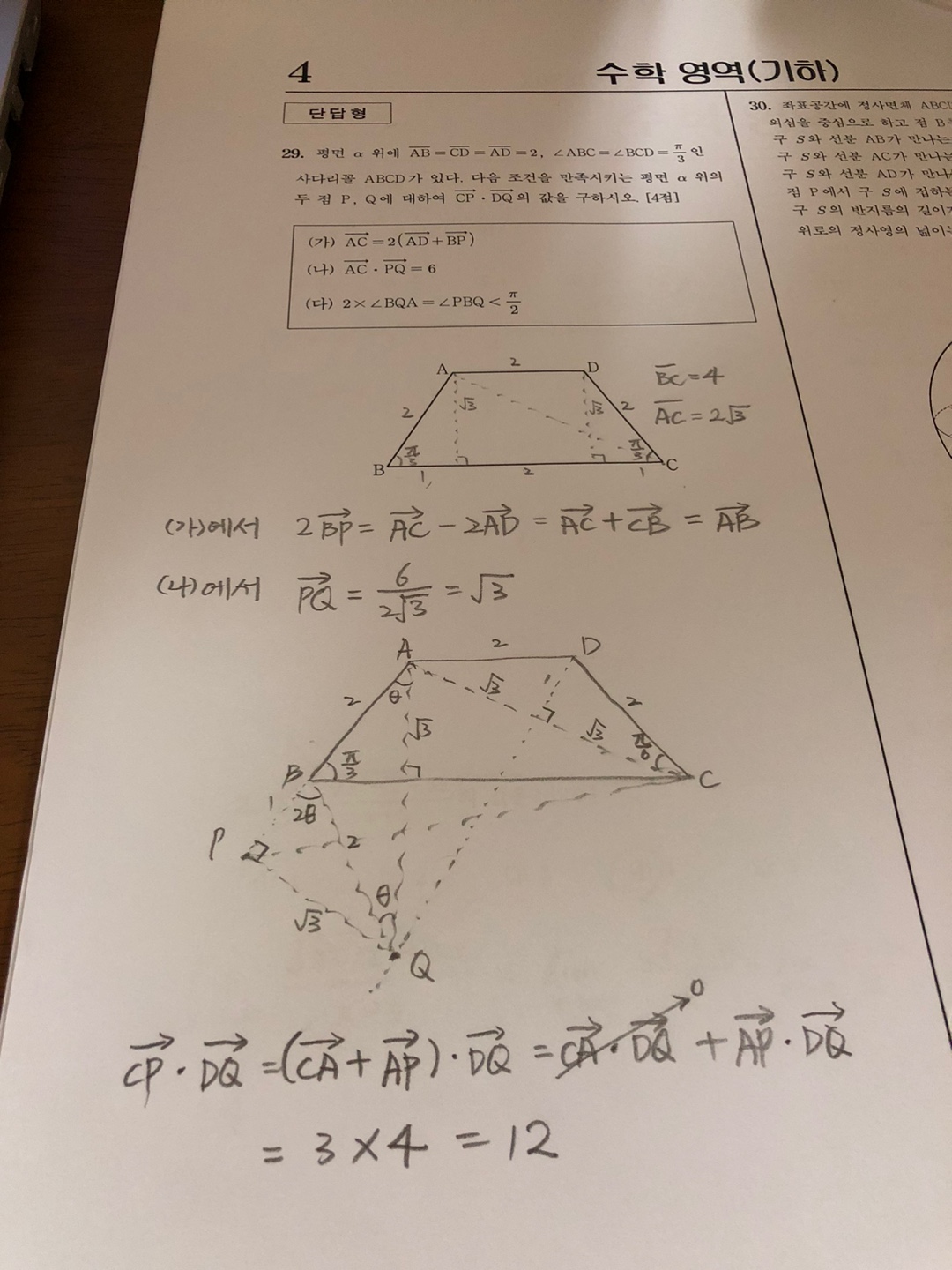
29번은 또 다시 벡터 문제가 나왔습니다. 평면 α 위에 사다리꼴 ABCD와 어디인지는 모르지만 점 P와 Q가 있습니다. 그냥 같은 평면 위라고 해도 되는데 굳이 평면 α라고 한 것은 불필요해 보입니다. 아무튼 사다리꼴의 모든 제원을 문제에서 줬습니다. AB=CD=AD=2이고 각도 ABC=BCD=π/3라고 했으므로 사다리꼴의 모든 길이 값은 제가 그린 것과 같이 모두 알 수가 있습니다. 29번 문제라고 하면 몇 번 꼬아서 낼만도 한데 너무 친절해서 당황스러울 정도였습니다.
그리고 동일 평면 위의 임의의 점 P와 Q에 대한 단서를 3가지 조건으로 제시했습니다. (가)부터 살펴보겠습니다. 벡터 AC=2(AD+BP)라고 했는데 우리는 이미 AC와 AD를 알고 있습니다. 정리해보면 BP=(AC-2AD)/2 입니다. 벡터의 성질을 이용하면 2AD= BC = -CB입니다. 그럼 벡터 BP=(AC+CB)/2 = AB/2 = 1이 됩니다. 게다가 벡터 AB의 1/2이므로 벡터 BP는 방향은 같고 길이가 절반인 벡터라는 것을 알 수 있습니다.
(나)에서는 벡터의 곱이 제시되었습니다. 벡터 AC·PQ=6, 벡터 PQ=6/AC=6/(2√3)=√3으로 정리할 수 있습니다. 여기서 우리는 벡터 AC는 벡터 PQ와 평행하다는 것을 알 수 있습니다. (가)와 (나)에서 벡터 BP가 벡터 AB와 방향이 같고 길이는 절반이고, 벡터 PQ는 벡터 AC와 평행하므로 제가 그린 것 처럼 될 수밖에 없다는 것을 알 수 있습니다. 그려놓고 조건 (다)를 살펴보겠습니다. 2 X ∠BQA = ∠PBQ < π/2 라고 했습니다. ∠BQA=θ, ∠PBQ=2θ라 할 때, ∠BAQ=θ가 됩니다. 삼각형 ABQ가 이등변 삼각형인 것을 알았으므로 AQ= 2√3이라는 것을 알 수 있습니다. 물론 삼각형 APQ에서 AP=3, PQ=√3이므로 피타고라스의 정리로 구할 수도 있습니다.
최종 문제는 CP·DQ 벡터의 곱을 구하는 것입니다. 벡터 DQ는 삼각형 DAQ에서 DA=2, AQ= 2√3이므로 피타고라스 정리에 의해 벡터 DQ=4라는 것을 쉽게 알 수 있지만, 벡터 CP는 주어진 조건만으로는 알기 어렵습니다. 그래서 출제 위원들이 벡터 문제로 낸 것입니다. 벡터 DQ도 먼저 풀지 말고 기다렸다가 풀면 됩니다. 벡터 CP=CA+AP로 바꿀 수 있으므로 벡터의 곱은 이렇게 정리할 수 있습니다. CP·DQ = (CA+AP)·DQ = CA·DQ + AP·DQ에서 CA·DQ는 두 벡터가 수직이기 때문에 0이 됩니다. 삼각형 ADC가 이등변 삼각형이고, 벡터 AC와 벡터 PQ가 평행하며, 벡터 AC=2PQ이기 때문에 수직일 수밖에 없습니다. 따라서 CP·DQ = AP·DQ = 3X4=12가 정답입니다.
'잡학다식 & 자료 창고' 카테고리의 다른 글
| [엔지니어가 취미로 푸는 수학] 2023년 수능 수학 손글씨 문제 풀이 풀버전 스캔 파일 다운로드 (0) | 2023.03.08 |
|---|---|
| [엔지니어가 취미로 푸는 수학] 2023년 수능 수학 홀수형 기하학 30번 문제 풀이 (1) | 2023.03.07 |
| 2021년도 주거실태조사 결과 발표 (0) | 2023.03.06 |
| [엔지니어가 취미로 푸는 수학] 2023년 수능 수학 홀수형 기하학 28번 문제 풀이 (0) | 2023.03.05 |
| [엔지니어가 취미로 푸는 수학] 2023년 수능 수학 홀수형 기하학 27번 문제 풀이 (0) | 2023.03.04 |





댓글 영역