고정 헤더 영역
상세 컨텐츠
본문

2023년 수능 수학 홀수형 공통 16번 문제입니다. 주관식 문제가 시작되었네요. 로그의 기본만 알면 간단히 풀 수 있는 문제입니다. 로그와 지수의 변환, 로그의 덧셈, 상수의 로그 변환 등의 기본 원리만 이해하면 됩니다. 로그 함수는 지수 함수의 역함수이고 로그 함수의 결과값이 지수가 됩니다. 따라서 상수 2는 로그 밑의 수가 2이므로 밑의 수가 2인 log4로 변환되고 밑의 수가 같은 로그의 덧셈은 곱셈으로 처리됩니다. 따라서 등식이 성립하려면 양변의 로그 위의 수끼리 같아야 하므로 방정식으로 계산하면 됩니다. 이런 문제만 나오면 좋겠습니다.
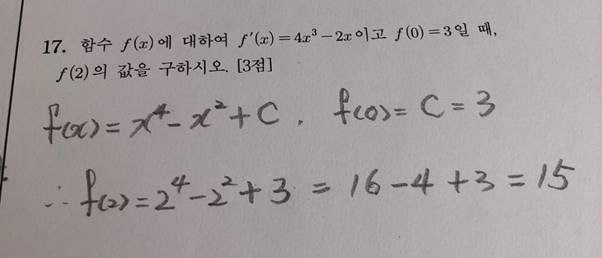
2023년 수능 수학 홀수형 공통 17번 문제입니다. 적분의 기본만 알면 풀 수 있는 문제입니다. 부정적분으로 상수 C가 필요한데, f(0)=3이라는 것을 문제에서 주어졌기 때문에 간단히 적분 상수 C를 구할 수 있습니다. 이제 f(x)를 알았으므로 x=2만 대입해서 풀면 되는 간단한 문제입니다. 이 문제는 그냥 3점 주려고 낸 문제인 것 같습니다. 하지만 방심은 금물입니다. 쉬운 문제일수록 검산을 해봐야 합니다. 실제로 저는 고등학교 때 2의 4승을 16이 아니라 64라고 계산해 놓고 검산도 안해서 틀린 적도 있었습니다. 너무 당연히 맞았다고 생각해서 자만한 결과였습니다. 수학은 이와 같이 실수를 최소한으로 하는 것이 잘하는 것입니다. 아무리 아는 것이 많아도 실수가 많으면 잘하는 것이 아닙니다.

2023년 수능 수학 홀수형 공통 18번 문제입니다. 수열의 합에 관한 문제입니다. 나름 3ak + 5와 같이 등차수열과 등비수열을 합쳐놓은 듯한 형태로 주어졌습니다. 역시 수열의 합에 대한 기본 개념만 알면 되는 문제입니다. 결국 시그마 ak를 구할 수 있는지를 묻는 문제입니다. 1부터 5까지 수열 5개만 더하는 문제이므로 연상하기에도 편리합니다. 이런 문제만 계속 나왔으면 좋겠습니다.
수열의 합에서 조심해야 할 것은 상수의 처리입니다. 여기서는 5인데 그냥 단순히 괄호 밖으로 나가서 계산했다가는 틀립니다. 그래서 저는 조심하기 위해서 일부러 수열을 풀어 쓰면서 정리한 것입니다. 저도 고등학교 때 이런 실수를 정말 많이 했었기 때문에 몸에 습관이 밴 것 같습니다. 역시 수학은 시행착오를 많이 겪어봐야 하고, 여기서 시행착오란 많이 틀리고 많이 좌절해봐야 한다는 의미입니다. 그래서 제가 맨날 얘기하는 것과 같이, 수학은 그래서 우리 인생을 닮았습니다. 많이 틀려보고, 많이 실패한 만큼 성장하게 되어 있습니다. 수학을 만점 받은 친구가 있다면 그 친구는 세상 누구보다 많이 틀려봤던 친구일 것입니다. 수많은 시행착오와 좌절감을 견뎌낸 결과로 좋은 성적을 받았을 것입니다. 가우스 형님이나 오일러 형님 같은 시대를 관통하는 수학 천재들이 아닌 이상 그게 정상입니다.
'잡학다식 & 자료 창고' 카테고리의 다른 글
| [엔지니어가 취미로 푸는 수학] 2023년 수능 수학 홀수형 공통 20번 문제 풀이 (0) | 2023.02.06 |
|---|---|
| [엔지니어가 취미로 푸는 수학] 2023년 수능 수학 홀수형 공통 19번 문제 풀이 (0) | 2023.02.05 |
| [엔지니어가 취미로 푸는 수학] 2023년 수능 수학 홀수형 공통 15번 문제 풀이 (0) | 2023.02.03 |
| [엔지니어가 취미로 푸는 수학] 2023년 수능 수학 홀수형 공통 14번 문제 풀이 (3) | 2023.02.02 |
| [엔지니어가 취미로 푸는 수학] 2023년 수능 수학 홀수형 공통 13번 문제 풀이 (0) | 2023.02.01 |





댓글 영역