고정 헤더 영역
상세 컨텐츠
본문

2023년 수능 수학 홀수형 확률과 통계 23번 문제 풀이입니다. 이 문제를 보자마자 곧바로 풀이를 시작했습니다. 5제곱이므로 그냥 하면 되겠거니 하고 아무 생각없이 풀기 시작했습니다. 중간쯤 풀었을 때 뭔가 느낌이 이상했습니다. 이 문제가 확률과 통계에 왜 나왔지? 분명히 뭔가 이상했습니다. 하지만 이미 중간쯤 풀었으니 일단 마무리하기로 했고, 나중에 더 편한 방법이 있다면 검증용으로 사용하자고 마음 먹었습니다. 아마 문제를 출제하신 분들도 공식 모르면 직접 풀어서라도 답을 찾아보라는 취지로 5제곱만 문제로 낸 것 같습니다. 만약 공식만이 목적이었다면 10제곱 이상을 냈을 것 같습니다. 그렇게 일단 다 풀고 나서 인터넷으로 검색을 해보니 순열과 조합에서 조합 (Combination)을 이용해서 푸는 방법이 있었습니다. 이때의 조합은 이항계수와 동일합니다. 어떤 순서로 뽑았는지 상관없기 때문입니다.
이 문제를 풀기 위해 사용되는 확률과 통계의 개념은 이항정리입니다. 이항정리의 정의는 다음과 같습니다.
이항정리 (二項定理, binomial theorem)
(a+b)n (n은 음이 아닌 정수)의 꼴을 전개할 때 쓰이는 정리이다. 이항정리의 '이항'은 '두 개의 항(二項)'이라는 뜻이며, '항을 옮긴다'(移項)는 뜻이 아니다. 이것의 증명에는 파스칼의 정리를 이용하는 방법과 테일러 급수를 이용하거나, 경우의 수를 이용하는 방법이 있다.
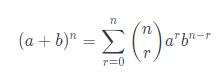
위 기본 공식에서 시그마와 행렬 부분을 조합 (Combination)으로 치환할 수 있으므로 위에서 제가 푼 것처럼 풀 수 있습니다. 혹시 이 문제를 보고 x의 8승의 계수를 구하면 어떡해야 할지 고민하시는 분들도 계실 수 있어서 말씀 드리는데 x의 3승의 5제곱에서는 x의 8승은 존재할 수가 없습니다. 3승의 거듭제곱이어야 하므로 3의 배수의 지수만 가질 수 있으니 그런 걱정은 할 필요가 없습니다. 열심히 수학을 공부하시는 분들은 그럴 리가 없겠지만 요즘 세상이 하도 말이 안 되는 일들이 일어나고 있으니 혹시나 해서 노파심에 말씀 드렸습니다.
'잡학다식 & 자료 창고' 카테고리의 다른 글
| [엔지니어가 취미로 푸는 수학] 2023년 수능 수학 홀수형 확률과 통계 24번, 25번 문제 풀이 (0) | 2023.02.10 |
|---|---|
| 2020년 대한민국 아름다운정원 콘테스트 화보집 (0) | 2023.02.10 |
| [엔지니어가 취미로 푸는 수학] 2023년 수능 수학 홀수형 공통 22번 문제 풀이 (0) | 2023.02.08 |
| 지속가능경영을 위한 기업 가이드 ESG A to Z (0) | 2023.02.08 |
| [엔지니어가 취미로 푸는 수학] 2023년 수능 수학 홀수형 공통 21번 문제 풀이 (0) | 2023.02.07 |





댓글 영역