고정 헤더 영역
상세 컨텐츠
본문
엔지니어가 취미로 푸는 수학

2023년 수능 수학 홀수형 기하학 25번 문제 풀이
2023년 수능 수학 홀수형 기하학 25번 문제 풀이입니다. 이번에는 기하학 중에서 타원 문제입니다. 타원은 무조건 초점만 제대로 알면 됩니다. 아래 왼쪽 그림을 보시면 되며, 그래프 상으로 장축 2a와 단축 2b를 갖고 초점을 (-c, 0)과 (c, 0)을 가지면 타원이 됩니다. 이때 축과 초점 사이의 관계는 C^2=a^2-b^2입니다. 오른쪽 그림은 반대로 장축 2b와 단축 2a를 갖고 초점을 (-c, 0)과 (c, 0)이며, 이때 축과 초점 사이의 관계는 C^2=b^2-a^2입니다.
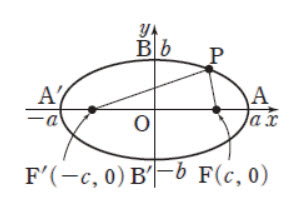
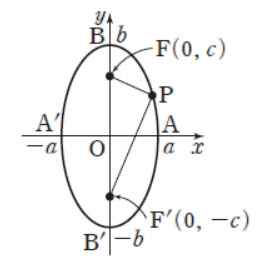
여기서 주의할 점은 왼쪽이든 오른쪽이든 타원의 방정식은 변하지 않는다는 점입니다. 그리고 타원 위의 임의의 점 P에서 초점까지의 거리의 합은 장축의 길이와 항상 같습니다. 즉, PF + PF' = 2a (왼쪽) 또는 2b (오른쪽)가 성립해야 합니다. 이것만 알면 타원 문제는 풀 수 있습니다.
문제로 다시 돌아가 보면, 전형적인 타원 방정식이 주어졌고, 타원 위의 임의의 한 점의 좌표도 주어졌습니다. 그리고 특이하게 타원 상의 한 점에서의 기울기가 주어졌습니다. 그러면서 두 초점 사이의 거리를 구하는 문제입니다. 두 초점 사이의 거리를 구하려면 일단 a와 b 값을 알아야 하고, 그러면 자연스럽게 왼쪽의 경우인지 오른쪽의 경우인지가 밝혀지게 될 것입니다. 문제에서 주어진 임의의 한 점으로부터 식 하나를 세울 수 있습니다. 이 식을 ①이라 하고, 두번째 조건에서 기울기가 주어졌으므로 양변을 모두 미분하면 됩니다. 이때 x=2일 때 기울기인 y'=1/2이라고 했으므로 두 값을 대입하면 식 ②를 얻을 수 있습니다. 식 ②에서 우리는 a가 b보다 크다는 것을 알 수 있습니다. 그렇다면 왼쪽의 경우에 해당합니다.
①과 ②를 연립하여 풀어보면 a^2=8, b^2=2를 구할 수 있습니다. 어차피 다시 제곱할 것이므로 루트를 씌울 필요는 없을 것 같습니다. 타원의 기본 성질 상 c^2 = a^2 - b^2이므로 계산이 금방 됩니다. 정답은 2 루트 6입니다.
만약 주관식이었다면 루트 6만 쓰고 다 풀었다고 실수할 수 있으니 주의해야 합니다. 문제가 원하는 정답은 두 초점 사이의 거리이지 c값을 구하는 것이 아니기 때문입니다. 아무리 단순한 문제라도 풀고나서 검산도 해보고 원하는 정답이 이게 맞는지 꼼꼼하게 문제를 다시 읽어보는 습관을 들여야 합니다. 자주 말씀 드리지만, 아프더라도 시행착오를 몇 번 겪어야 몸에 습관이 생깁니다. 그래서 출제자들도 마지막에 항상 그런 식으로 끝맺음하는 경우가 많습니다. 다 구한 뒤, '서로소이다', '두 값의 합을 구하라', '반올림하라' 등과 같이 말입니다. 세상 모든 일이 다 그렇지만 틀리고, 실패하고 좌절하는 횟수만큼 성장합니다. 극복하고 묵묵히 견디는 법을 배워야 합니다. 수학 좋아하는 꼰대가 한 말씀 드렸습니다. :)
'잡학다식 & 자료 창고' 카테고리의 다른 글
| [엔지니어가 취미로 푸는 수학] 2023년 수능 수학 홀수형 기하학 27번 문제 풀이 (0) | 2023.03.04 |
|---|---|
| [엔지니어가 취미로 푸는 수학] 2023년 수능 수학 홀수형 기하학 26번 문제 풀이 (1) | 2023.03.03 |
| [엔지니어가 취미로 푸는 수학] 2023년 수능 수학 홀수형 기하학 23번, 24번 문제 풀이 (0) | 2023.03.01 |
| [엔지니어가 취미로 푸는 수학] 2023년 수능 수학 홀수형 미적분 30번 문제 풀이 (0) | 2023.02.28 |
| [엔지니어가 취미로 푸는 수학] 2023년 수능 수학 홀수형 미적분 29번 문제 풀이 (1) | 2023.02.27 |






댓글 영역